中间代码优化

代码优化的阶段

• 用户对源程序进行优化
• 编译器前端对中间代码进行优化
• 编译器后端对目标代码进行优化

代码优化的几个问题

• 优化的角度
  • 执行效率
  • 存储
• 优化也是耗时耗力的，是否有意义
  • 一次编译多次执行，有性价比
  • 一些领域要求对程序的执行效率要求高，如实时控制，导航系统等
• 程序的优化
  • 重构，等价变化，递归→非递归
• 编译器优化程序
  • 手工写汇编程序更快
  • 编译后的目标程序比手工汇编程序最多慢1.3倍

中间代码优化的分类

从优化的种类来看，中间代码的优化可有如下分类：

局部优化

• 循环上的优化
  • 循环不变式外提
  • 削减运算强度
• 基本块的优化
  • 常表达式节省
  • 公共子表达式节省

全局优化

全局数据流分析，从而使优化的效果更好。

数学上的优化

• 不计算的直接删去四元式
• 高运算强度的转化成低运算强度

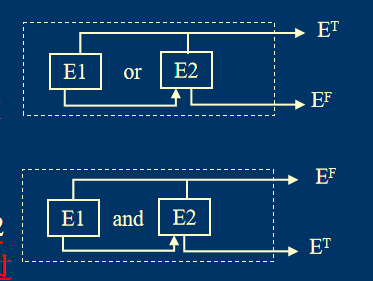
表达式短路问题

• `E=E1 or E2`
• `E=E1 and E2`

常表达式节省

常数提前计算出来，目标程序就不用计算了

公共子表达式节省

循环不变式外提

削减程序的运算强度

消除无用语句，消除冗余代码

寄存器优化

涉及到目标程序执行的时候，如何分配目标机的寄存器

中间变量优化

属于空间上的优化，假如两个临时变量的活动区不相交，则可以共用同一个

目标代码优化

通过确定目标代码减少目标程序指令个数来提高执行效率。譬如两个运算分类都在寄存器中，可以直接参与运算，不需要将其存入内存中导出运算

全局优化

对程序全局进行数据流分析，优化技术比较复杂

基本块的定义

• 基本块是指程序的一组顺序执行的语句序列，其中只有一个出口和一个入口
  • 入口：基本块的第一条语句
  • 出口：基本块的最后一条语句

基本块的特点

• 对于一个基本块而言，执行时只能从入口进，出口出
• 一个基本块内部的语句要么全执行，要么全不执行，不能执行其中的一部分，不能在中间转出，也不能从中间转入
• 基本块的划分可以基于源代码，中间代码和目标代码

为什么在基本块上优化

• 因为基本块中变量的性质是可以判定
• 基本块内顺序执行，变量的值怎么获得，如何传播，都能判定
• 优化的最重要原则是一定不能出错，可能出错就不优化

基本块的划分原则

• 整个四元式序列的第一个四元式为基本块的入口
• 遇转移性四元式时，结束当前基本块，并把该四元式作为当前基本块的出口，下一条四元式作为新基本块的入口

• 遇标号性四元式时结束当前基本块，四元式本身作为新基本块的入口

• 遇到对地址引用型变量赋值四元式时，结束当前基本块，并作为该块的出口
  • 初始开始
  • 遇跳转结束
  • 遇标号新开始，防止有两个入口
  • 遇地址结束

程序流图

常表达式节省

公共表达式节省

• 两个表达式中的子表达式他们的计算结果相同
  • 子表达式运算符w相同，且左右分量值相同
• 公共表达式节省在局部进行的时候都是针对基本块的

1:(w[1],a,b,t[1])
2:(w[2],c,d,t[2])
if w[1] == w[2] && a.value()==c.value() && b.value()==d.value():
    1和2为公共表达式

如何找到公共表达式

基于值编码的公共表达式节省

对中间代码中出现的每个值确定一个编码，使得具有相同值的运算分量对应的编码相同，一个值→一个编码

值编码的分配->值编码表
四元式的值编码表示->四元式映象码
优化后四元式的变化->中间变量等价表
(+,b,c,t)->(+,(1),(2),t)

• 编码原理：
  • 用到一张值编码表，表示分量当前值的编码
  • dk:(w,u1,u2,u3)
    • 若值编码表中已有(ui,mi) 则令dk:ui 的值编码为mi
    • 否则为dk:ui创建一个新编码m填入编码表
  • 若考察代码为dk:(=,u1,-,u2)
    • 令dk:u2的编码与dk:u1的编码相同
• 值编码性质：
  • u1处理与之前相同
  • 相同常量一定具有相同值编码
  • 不同常量的编码值一定不同
  • 不同分量上相同变量未必具有相同编码
  • 每当一个变量被x赋值，x将得到一个新的编码，使得后面代码中的x分量区编码值n，直至x再被赋值

循环不变式外提

• 如果一个表达式再一个循环中不改变其值，则称它为该循环的不变表达式
  • 表达式左右分量的值在循环中不被改变
• 循环不变式外提：将循环不变式提到循环外进行
• 同样也是针对运算型表达式（不对赋值等其他四元式外提）
• 思想
  • 第一遍：看哪些变量的值变了（建立定值表）
  • 第二遍：确定哪些没变（进行外提）
• 解决两个问题
  • 检查循环体中哪些变量的值被改变过
  • 根据这个结果来看哪些表达式是不变的表达式
• 建立变量定值表LoopDef，将循环体中值被改变的变量都填到表里，若某运算型四元式中两个运算分量都不出现在这个表里，就说明其值不发生改变，可以进行外提
• 把循环体四元式进行第一遍扫描，把有定值的变量填到变量定值表中，若是(w,A1,B1,t1) ,则把t1填到表中，若为赋值型四元式(=,a,-,b)则把b填入表中
• 把循环不变式外提为第二遍扫描，每遇到一个运算型四元式(w,A1,B1,t1) ,若A1，B1都不在变量定值表中，则将其提到循环体外，同时在变量定值表中删去t1

需要注意的问题

• 多层循环中，一个四元式从里层开始可以被外提若干次，里层变量定值表属于外层变量定值表。
• 除法不外提
• 赋值绝不外提
• 非良性循环（循环体有函数调用或地址引用型变量的赋值）不做外提优化，没法构造准确的变量定值表
• 运算四元式的运算分量是间接寻址时，四元式不外提，地址加运算可以外提